Cryptarithms
Cryptarithms, or alphametic puzzles, are arithmetic formulas where the digits have been replaced by letters or sometimes other symbols. If you are already familiar with the rules and logic required to solve these puzzles, you might like to skip to the worksheets below.
Rules
Just as in a cryptogram, each different letter corresponds to a different number and all instances of a particular letter corresponds to a particular number.
There should be only one possible solution to each cryptarithm.
The left most digit in each line is never a zero.
Example
Here is a popular cryptarithm. See if you can solve it on your own, or follow along below to see how I solved it.
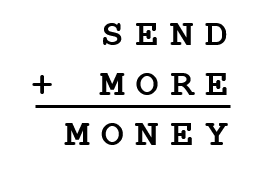
How to Solve a Cryptarithm
These mathematical puzzles require you to use logic and they can get pretty twisted. However, there are a few patterns that are oft repeated in arithmetic which you will see over and over when solving these puzzles.
STEP 1:
When adding just two numbers together, the most you will ever carry is 1, so we can reason that M must be a 1.

STEP 2:
The O is the next letter to consider. It can not be 1, because we have already used that number. If it were 2, S would be either 10 or 11 (since in the thousands column we have either S+1=O+10, or S+1+1=O+10 - in the case where a 1 is carried from the hundreds column), which is not allowed since these are two digit numbers. If O were greater than 2, S would be even larger. Therefore, the O is 0.

STEP 3:
In order for the 1 to be carried from the thousands column, the S now needs to be 8 or 9. If it is an 8, we would have to carry 1 from the hundreds column, so let's look at the hundreds column. We know that E cannot equal N, so we know there is 1 carried from the tens column. So for the hundreds column we have 1 + E + 0=N(+10?). We know the N has to be at least 2 (because 0 and 1 are taken), so in order for something to be carried 1 + E + 0 would need to be 12 or more. This would mean E would need to be 11 or more, which of course is not allowed, so nothing can be carried from the hundreds column, and thus S must be 9 rather than 8. Whew!

STEP 4:
Next we solve for the letter R. We already know that E+1=N and that 1 is carried from the tens column to the hundreds column. So we can substitute E+1 for N in the tens column to form two possible equations: E+1 + R=E+10 OR E+1 +1 + R=E+10 (the second equation includes carrying 1 from the ones column). The first equation give R=9, which is not possible because 9 is already accounted for. The second equation gives R=8, so R is 8.

STEP 5:
Consider the D and E. We know they must total 12 or more (a 1 is carried from the tens column and Y must be 2 or more since the 0 and 1 are taken). What digits are left that total 12 or more? We can not use 3 because 9 is taken, and we cannot use 4 because 8 is taken. We are left with 5,6, and 7. Since D and E need to be different numbers they must be 5 and 7, or 6 and 7. Now recall that E+1=N. If E were 7, N would be 8 which is already taken. If E were 6, N would be 7 and there is only 5 left for D, which is not enough (E + D would be less than 12). Therefore E is 5 and D is 7.

STEP 6:
Since we know that E is 5 and N=E+1, we know N=6. From here it is a simple matter of replacing the N with 6 and doing the addition.

Clear as mud, right? If you would like another explanation of this same problem and further explanations and tips on solving cryptarithms have a look at these examples worked out by master puzzlists.
Cryptarithm Worksheets
As you can see, these puzzles can be really tricky. They are excellent tools to hone logic skills, but not great for practicing arithmetic. So don't give them to beginning math learners. Even though I have marked the first of these worksheets "Beginner", these puzzles all require quite a bit of time and reasoning to solve. Lots of fun!




